Anybody who’s spoken to me about maths will have quickly learnt that I’m obsessed with multi-link blocks. In fact the last time I had a job interview, I inadvertently spent 15 minutes talking about them and the Cbeebies programme ‘Numberblocks’.

A 2 x 4 block ‘Octoblock’

In moments of insanity I have claimed that every topic taught in high school maths could be taught with the blocks. And so here, in this blog, I try to make good on my mad proclamations.

The Difference of Two Squares

I was playing with my (then) four-year-old, who was putting the blocks together. She had 100 blocks in front of her and she was building in a pleasing way, producing bigger and bigger squares. But to my horror when she had a 10×9 rectangle, she opted for adding an eleventh column. I tried to encourage a 100 square, but the girl had her own opinions. When she finished her 11×9 rectangle she found she had one cube left over and she was very cross.

a 9 by 11 block, with 1 clock left over One Left Over

This got me thinking about how things would have turned out if she had gone off-piste sooner. Would a 12×8 rectangle have two blocks left over? Of course we know that twelve eights are 96 so there would be 4 blocks left over.

8 x 12 block with 4 left over 4 left over

What about a 13×7 rectangle? Well seven thirteens are 91, so 9 left over.

1, 4, 9… Hang on, these are square numbers!

Does that mean that 5×15 would leave 25 blocks from 100? Well indeed it does!

The natural question that follows is: Is this a special feature of 100, or would it work with any starting number of blocks?

Let’s try a 12 by 12 square. That’s 144 blocks. How many spare blocks do you have if you make a 10×14 rectangle? 10 and 14 are two away from twelve, so our conjecture is there should be 2×2=4 spare blocks. We know that 10×14 = 140 and so it works.

Now the fun begins- we have a quick way to solve tricky looking multiplications, mentally, in seconds.

What’s 35×45? Well, 40 x 40 is 1600. 35 and 45 are 5 away from 40. So we just work out 1600-25= 1575.

Any multiplication where the two factors are equidistant from a multiple of 10 becomes easy. 58×62 = 3600-4 = 3596.

So naturally I felt quite pleased about all this. Until I came to prove it; when I suddenly felt incredibly stupid.

Let’s call the number of bricks you start with x squared. Let’s say “a” is the distance from x.

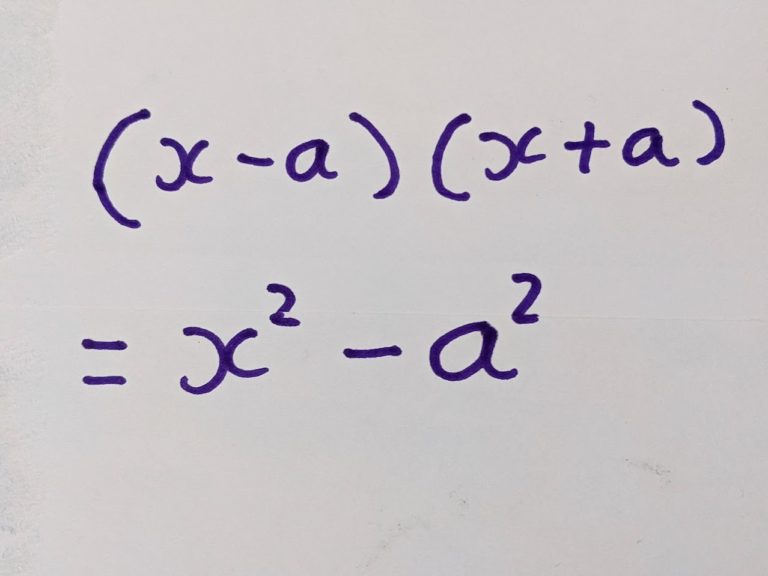
Our conjecture is: (x-a)(x+a) = x squared - a squared

There’s nothing like maths to sometimes make you feel a bit stupid is there? I didn’t realise what I was writing out until I had finished writing it.

I like this story because before I played with the blocks, the difference of two squares was a bit of a boring consequence of expanding brackets. A special case of factorising a trinomial. Thanks to a stubborn child, it’s all more interesting now.